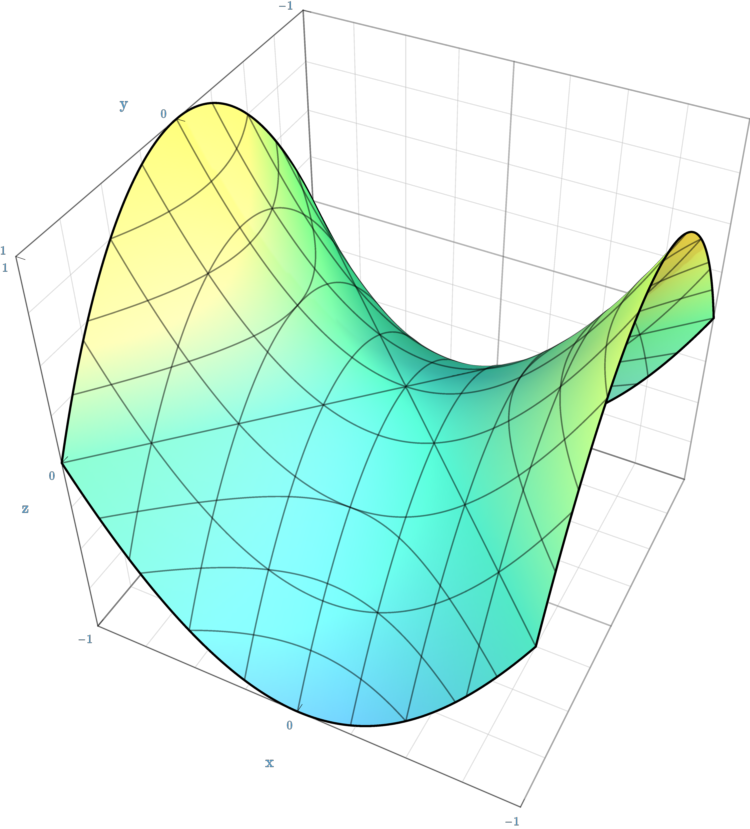
Math: line intersections
Lately a lot of my shaders have used a bit of raymarching, where I primarily rely on finding the intersections between a line (ray) and a shape. In this post I will go over the general approach for calculating these intersections and provide a list of HLSL implementations. The shapes discussed here will include planes, quadric surfaces (e.g. a sphere) and some useful combinations of them.
This tutorial was made with Unity 2020.3.1f1 and the Universal Render Pipeline (URP). Note that the general concept can be applied to any shader or coding environment. You can download the finished HLSL file, including an example shader, as Unity package through my git repository. If you’ve never imported a Unity package via a git repository this documentation will be helpful.
Acknowledgements
As this is mostly a tutorial on mathematics and its implementation my main acknowledgement would be my university level classes in Calculus and Linear Algebra. For those interested I shall list the Calculus book I’ve used, but know that I’ve put plenty of links to the relevant wiki articles throughout this tutorial as well.
- Calculus: A Complete Course (8th edition), by Robert Adams and Christopher Essex.
Contents
1 Finding intersections
The method for finding line intersections that I will discuss here relies on knowing a general equation for a shape and substituting it’s coordinates with a parameterised line.
Starting with what a parameterised line is. It is defined solely by an origin and a direction that scales with a parameter (a number that can be anywhere between negative and positive infinity). The points on this line are given by the equation \(\overrightarrow{P} = \overrightarrow{O_L} + \overrightarrow{D_L} t\). Here \(\overrightarrow{O_L}\) is the origin, \(\overrightarrow{D_L}\) the direction and \(t\) the parameter. Our parameter t thus denotes the distance from our line’s origin along the direction and can be anywhere between negative and positive infinity.
For those unfamiliar with the notation, the arrows denote vectors with an x, y and z component, like \(\overrightarrow{P} = \begin{pmatrix} P_x \\ P_y \\ P_z \end{pmatrix} = \begin{pmatrix} O_x + D_x t \\ O_y + D_y t \\ O_z + D_z t \end{pmatrix}\).
Now to find the intersections between this line and a shape we need to know the shape’s equation, substitute it’s x, y and z component with \(\overrightarrow{P}\), and solve for \(t\). For example, the equation of a sphere would be \(x^2 + y^2 + z^2 = r^2\), with \(r\) the radius. To find the intersections we would substitute \(x \rightarrow P_x\), \(y \rightarrow P_y\) and \(z \rightarrow P_z\). This would result in an equation that has only one variable, our parameter \(t\). Solving this equation for \(t\) would then give us the distance between the intersection and the line’s origin \(\overrightarrow{O_L}\) (if there is an intersection).
So to summarise, the method consists of the following 3 steps:
- Know or find the shape equation
- Substitute coordinates with the parameterised line equation
- Solve the equation for parameter t, the distance to the intersection
Note that this method will also return negative distances, i.e. when the intersection is behind the line’s origin. In most use cases you would either discard these negative distances or use it to say something about your location, e.g. if the shape is convex and there is one intersection behind you and one in front you are within the shape’s volume.
1.1 Space transformation
Most of our shapes will point in some direction, like a plane that has its normal pointing upward along the y-axis. For simplicity’s sake we will define each shape equation in its own local space where the shape is centred on the origin and y is always the up axis, z is the forward axis and x is the right axis.
In order to translate and rotate our shapes to any place or direction we will be transforming our input line (that is likely defined in world space) to our shape’s local space, somewhat similar to transforming from world space to object space except we don’t adjust the scale. In order to do this we will provide two orthonormal vectors that form a basis of our shape space, the forward and up direction, in addition to the origin of the shape. These vectors must be defined within the same space as our input line. With this transformation we can easily define our shapes in their local x, y and z coordinates and use a transformation matrix to rotate and the origin to translate the shape to any location/rotation we want.
In short, our equations will be defined in their own space, where it is centred on the origin and always pointing upward. However, our input is defined in world space (or any other space), which consists of the line’s origin, the line’s direction, the shape’s origin and the shape’s direction (up and forward vectors). Finally, we use the shape’s origin and direction to transform our line to shape space.
I know this might be a bit much and the next sections will show it implemented in code, but let me know if you want a more in-depth tutorial on matrix transformations. In the meanwhile you can also check out this tutorial by Catlike Coding on matrix transformations.
1.2 HLSL include file
The actual HLSL implemenation of our line intersections will be in the form of a HLSL include file that we can add to any shader. Create a new text file and change its name (including format) to “LineIntersections.hlsl” and add the following lines.
#ifndef LINE_INTERSECTIONS_INCLUDED
#define LINE_INTERSECTIONS_INCLUDED
float3x3 constructTransitionMatrix(float3 forwardDir, float3 upDir)
{
float3 rightDir = cross(forwardDir, upDir);
float3x3 result = {rightDir, upDir, forwardDir};
return result;
}
#endifThe constructTransitionMatrix function uses the shape’s forward and up direction to construct a rotation matrix to transform from our input space to the shape’s space. Notice the definition lines starting with a #. These are used to ensure that we don’t accidently include our functions twice in a shader. Basically, it checks if LINE_INTERSECTIONS_INCLUDED is defined, if not, define it and add our functions.
1.3 Plane intersection
Now onto the actual stuff, finding intersections. We’ll start with the simplest shape, as it always has exactly one intersection, the flat plane. We can define a plane with the following equation [1]:
Here the shape parameters \(\begin{pmatrix} s_x \\ s_y \\ s_z \end{pmatrix}\) determine the normal of the plane and \(s_t\) an offset along the normal. Now in order to find the intersection with the line we need to substitute our \(\begin{pmatrix} x \\ y \\ z \end{pmatrix}\) coordinates with the line parameterisation \(\overrightarrow{P} = \begin{pmatrix} O_x + D_x t \\ O_y + D_y t \\ O_z + D_z t \end{pmatrix}\). Because this is a simple linear equation we can solve it for t to find the distance between the line’s origin and the intersection. This process is written out below.
Because we’re transforming our line to the shape’s local space, which already defines the shape’s direction and origin/offset, we don’t have to provide the shape parameters as they overlap. In our shape space the plane always points up (the y-direction), this allows us to simplify the equation to \(t = -\frac{O_y}{D_y}\).
The code block below shows how this is implemented in HLSL, where we transform the input line to shape space and calculate \(t\). As input we provide the line origin, line direction, shape origin, and shape up direction. Add the following lines to our HLSL file below the constructTransitionMatrix function but before #endif.
// Based on plane equation from https://en.wikipedia.org/wiki/Plane_(geometry)#Point%E2%80%93normal_form_and_general_form_of_the_equation_of_a_plane
float intersectPlane(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeUpDir)
{
// Transform line origin and direction from world space to the shape space
float3x3 transitionMatrix = construcTransitionMatrix(float3(0,0,0), shapeUpDir);
float3 lO = mul(transitionMatrix, lineOrigin - shapeOrigin);
float3 lD = mul(transitionMatrix, lineDir);
float denominator = lD.y;
float numerator = lO.y;
return - numerator / denominator;
}In the previous section I noted we must always provide two orthonormal vectors, but because our plane is infinite and thus symmetric within the plane we can get away with only providing one vector, the normal or up direction.
1.4 Visualise shader
Having this LineIntersections.hlsl is great and all, but we can’t see anything yet as we do not have a shader or material. Let’s change that by making a new shader called VisualiseIntersection.shader and fill it with the code block below.
Shader "KelvinvanHoorn/VisualiseIntersection"
{
Properties
{
_ShapeParams ("Shape parameters", vector) = (1,1,1,1)
_DistanceScale ("Distance scale", float) = 100
_CapHeights ("Cap heights", vector) = (0,1,0,0)
}
SubShader
{
Tags { "RenderType" = "Opaque" "RenderPipeline" = "UniversalRenderPipeline" "Queue" = "Geometry" }
Cull Front
Pass
{
HLSLPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Core.hlsl"
#include "LineIntersections.hlsl"
struct Attributes
{
float4 posOS : POSITION;
};
struct v2f
{
float4 posCS : SV_POSITION;
float3 posWS : TEXCOORD0;
float3 objectOrigin : TEXCOORD1;
};
float4 _ShapeParams;
float _DistanceScale;
float2 _CapHeights;
v2f vert(Attributes IN)
{
v2f OUT = (v2f)0;
VertexPositionInputs vertexInput = GetVertexPositionInputs(IN.posOS.xyz);
OUT.posCS = vertexInput.positionCS;
OUT.posWS = vertexInput.positionWS;
// Object information
OUT.objectOrigin = UNITY_MATRIX_M._m03_m13_m23;
return OUT;
}
float4 frag (v2f IN) : SV_Target
{
// Line information
float3 lineOrigin = _WorldSpaceCameraPos;
float3 lineDir = normalize(IN.posWS - _WorldSpaceCameraPos);
// Shape information
float3 shapeUpDir = normalize(mul(unity_ObjectToWorld, float4(0,1,0,0)).xyz);
float3 shapeForwardDir = normalize(mul(unity_ObjectToWorld, float4(0,0,1,0)).xyz);
float3 shapeOrigin = IN.objectOrigin;
float r = 0;
float g = 0;
float b = 0;
// Intersect information
float intersect = intersectPlane(lineOrigin, lineDir, shapeOrigin, shapeUpDir);
if(intersect < maxLineDst && intersect > 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * intersect;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
return float4(r, g, b, 1);
}
ENDHLSL
}
}
}This tutorial is primarily focussed on the mathematics and implementation behind finding line intersections, I will thus only shortly gloss over what the shader does.
We use 3 properties to influence our shapes, the shape parameters which usually say something about the scale, the distance scaling which is used to colour the shape and the cap heights which will be used in section 3 for the cap positions.
We include our LineIntersections.hlsl file at line 21. The #include requires the path to our HLSL file, if this is in the same folder we can simply put the name there. Otherwise it would look something like the following.
#include "Assets/folder/subfolder/LineIntersections.hlsl"
// or if you're using the package
#include "Packages/com.kelvinvanhoorn.line-intersections/ShaderLibrary/LineIntersections.hlsl"We start our line at the camera’s world space location, with its direction being towards the fragment world position of the gameObject to which we apply the material. The shape’s origin is set to the gameObject’s origin and the shape’s forward and up direction are set to the gameObject’s local forward and up direction.
Finally we get the intersection information to determine the output colour. If there is an intersection and it is in front of the camera we colour it depending on its distance with respect to the shape’s origin, otherwise it is black to show the bounds of our gameObject.
I’ve applied the shader to a standard Unity sphere with all scales set to 50. The image below shows a visualisation of the plane intersection. The red and blue line correspond with the world x-axis and z-axis respectively.

2 Quadric surfaces
In the following sections I’ll go through the surface equations of quadrics and use the quadratic formula to find their intersections. Quadrics describe surfaces that are expressed as a polynomial of second degree, i.e. quadratic functions like the following.
When we substitute the line equation into a quadric equation it will also be quadratic in \(t\), and thus like any quadratic function it will have at most 2 intersections. Moreover, it means we can refactor it and use the quadratic formula to solve it.
You’ve probably already encountered the quadratic formula in a mathematics class. Basically we refactor a quadratic equation to a general form, calculate the discriminant (d) and use that to calculate the intersections. Written out this method consists of the following equations.
Note that depending on the discriminant there are either 2, 1 or no intersections, which respectively corresponds to \(d > 0\), \(d = 0\) or \(d < 0\).
Implementing this in HLSL is a straightforward copy of the mathematical equations, except that we need to decide on what to return if there are no intersections. In my case I’ve decided to return the maximum float value as we should never deal with an intersection that far away. Add the following lines to our HLSL file just above the constructTransitionMatrix function. We will use this function to solve all our quadric surface intersections.
static const float maxLineDst = 3.402823466e+38;
float2 quadraticFormula(float a, float b, float c)
{
float discriminant = b * b - 4 * a * c;
if (discriminant >= 0)
{
float s = sqrt(discriminant);
float minDst = (-b - s) / (2 * a);
float maxDst = (-b + s) / (2 * a);
return float2(minDst, maxDst);
}
// returns maxLineDst if no intersection
return float2(maxLineDst, maxLineDst);
}2.1 Elliptic cylinder

The first quadric to discuss is the elliptic cylinder, an infinite cylinder with two focal points, i.e. the x-z plane cross-section is an ellipse. The equation for an elliptic cylinder is as follows [3]:
Here the scale parameters \(s_x\) and \(s_z\) act similar to the radius of a circular cylinder. Substituting the line equation results in:
Refactoring this equation results in a quadratic function of form \(a t^2 + b t + c = 0\), with the following coefficients:
We can then use the quadratic formula from the previous section to find up to two intersections. The code below shows how this is implemented in HLSL. As input we provide the line origin, line direction, shape origin, shape forward direction, shape up direction, and the scale parameters \(s_x\) and \(s_z\). Add the following lines to our HLSL file below the intersectPlane function.
// Based on quadrics equations from https://en.wikipedia.org/wiki/Quadric
float2 intersectEllipticCylinder(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeForwardDir, float3 shapeUpDir, float2 scaleParams)
{
// Transform line origin and direction from world space to the shape space
float3x3 transitionMatrix = construcTransitionMatrix(shapeForwardDir, shapeUpDir);
float3 lO = mul(transitionMatrix, lineOrigin - shapeOrigin);
float3 lD = mul(transitionMatrix, lineDir);
// Squared reciprocals of the shape parameters s_x and s_z
float rsx = 1.0 / (scaleParams.x*scaleParams.x);
float rsz = 1.0 / (scaleParams.y*scaleParams.y);
float a = lD.x*lD.x * rsx + lD.z*lD.z * rsz;
float b = 2 * (lO.x * lD.x * rsx + lO.z * lD.z * rsz);
float c = lO.x*lO.x * rsx + lO.z*lO.z * rsz - 1;
return quadraticFormula(a, b, c);
}To visualise this intersection change the intersection information in our visualise shader to the following. We now determine the colour on the first intersection in front of the camera, as we get 2 values now instead of 1.
// Intersect information
float2 intersect = intersectEllipticCylinder(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, _ShapeParams.xz);
float frontIntersection = intersect.x >= 0 ? intersect.x : intersect.y;
if(frontIntersection < maxLineDst && frontIntersection >= 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * frontIntersection;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
2.2 Ellipsoid
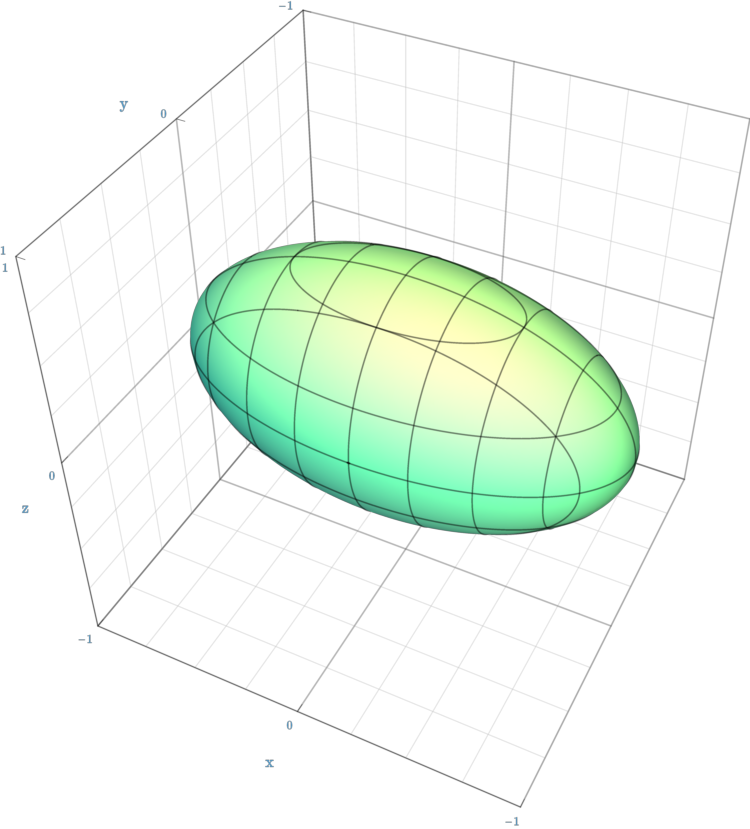
The ellipsoid is my most used quadric surface, as it includes the sphere where all axes have the same radius. The equation for an ellipsoid is given by the following [3]:
Here the scale parameters \(s_x\), \(s_y\) and \(s_z\) act similar to the radius of a sphere. Substituting the line equation results in:
Refactoring this equation results in a quadratic function of form \(a t^2 + b t + c = 0\), with the following coefficients:
Using the quadratic formula we can find up to two intersections. The code below shows how this is implemented in HLSL. As input we provide the line origin, line direction, shape origin, shape forward direction, shape up direction, and the scale parameters \(s_x\), \(s_y\) and \(s_z\). Add the following lines to our HLSL file below the intersectEllipticCylinder function.
// Based on quadrics equations from https://en.wikipedia.org/wiki/Quadric
float2 intersectEllipsoid(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeForwardDir, float3 shapeUpDir, float3 scaleParams)
{
// Transform line origin and direction from world space to the shape space
float3x3 transitionMatrix = constructTransitionMatrix(shapeForwardDir, shapeUpDir);
float3 lO = mul(transitionMatrix, lineOrigin - shapeOrigin);
float3 lD = mul(transitionMatrix, lineDir);
// Squared reciprocals of the shape parameters
float rsx = 1.0 / (scaleParams.x*scaleParams.x);
float rsy = 1.0 / (scaleParams.y*scaleParams.y);
float rsz = 1.0 / (scaleParams.z*scaleParams.z);
float a = lD.x*lD.x * rsx + lD.y*lD.y * rsy + lD.z*lD.z * rsz;
float b = 2 * (lO.x * lD.x * rsx + lO.y * lD.y * rsy + lO.z * lD.z * rsz);
float c = lO.x*lO.x * rsx + lO.y*lO.y * rsy + lO.z*lO.z * rsz - 1;
return quadraticFormula(a, b, c);
}To visualise this intersection change the intersection information in our visualise shader to the following.
// Intersect information
float2 intersect = intersectEllipsoid(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, _ShapeParams.xyz);
float frontIntersection = intersect.x >= 0 ? intersect.x : intersect.y;
if(frontIntersection < maxLineDst && frontIntersection >= 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * frontIntersection;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
2.3 Hyperboloid
 Hyperbolic hyperboloid [2] \(s_t > 0\)
Hyperbolic hyperboloid [2] \(s_t > 0\)
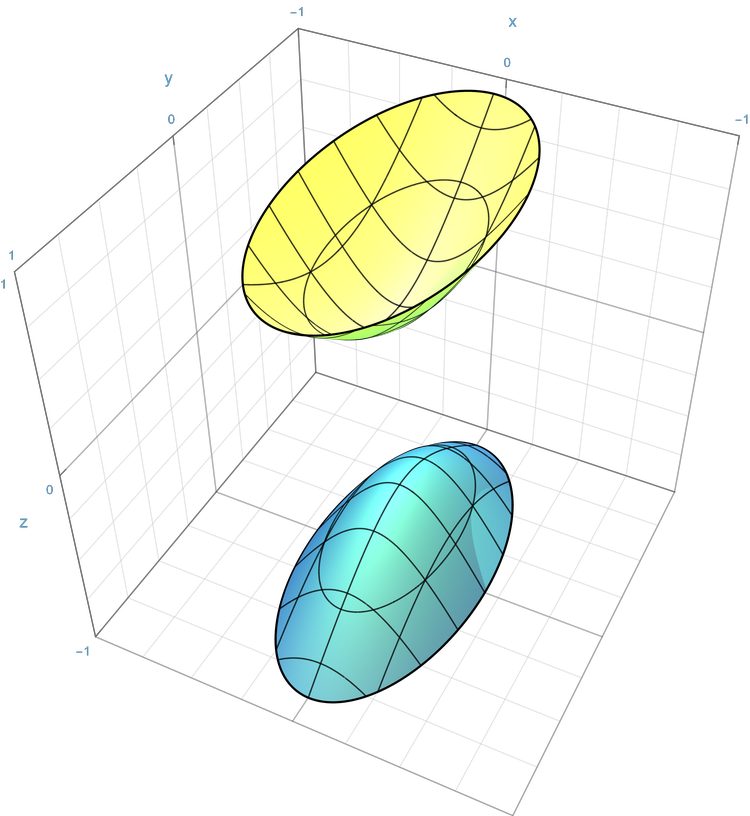 Elliptic hyperboloid [2] \(s_t < 0\)
Elliptic hyperboloid [2] \(s_t < 0\)
The hyperboloid equation is very similar to the ellipsoid, except that the y component is negative and that we have an additional parameter for type (\(s_t\)). Depending on this type parameter we can have a hyperbolic (\(s_t > 0\)) or elliptic (\(s_t < 0\)) hyperboloid or an elliptic cone (\(s_t = 0\)). The equation for hyperboloids is given by the following [3]:
By substituting the line equation we get:
Refactoring this equation results in a quadratic function of form \(a t^2 + b t + c = 0\), with the following coefficients:
Using the quadratic formula we can find up to two intersections. The code below shows how this is implemented in HLSL. As input we provide the line origin, line direction, shape origin, shape forward direction, shape up direction, the scale parameters \(s_x\), \(s_y\) and \(s_z\), and the type parameter \(s_t\). Add the following lines to our HLSL file below the intersectEllipsoid function.
// Based on quadrics equations from https://en.wikipedia.org/wiki/Quadric
float2 intersectHyperboloid(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeForwardDir, float3 shapeUpDir, float3 scaleParams, float typeParam)
{
// Transform line origin and direction from world space to the shape space
float3x3 transitionMatrix = constructTransitionMatrix(shapeForwardDir, shapeUpDir);
float3 lO = mul(transitionMatrix, lineOrigin - shapeOrigin);
float3 lD = mul(transitionMatrix, lineDir);
// Squared reciprocals of the shape parameters
float rsx = 1.0 / (scaleParams.x*scaleParams.x);
float rsy = 1.0 / (scaleParams.y*scaleParams.y);
float rsz = 1.0 / (scaleParams.z*scaleParams.z);
float a = lD.x*lD.x * rsx - lD.y*lD.y * rsy + lD.z*lD.z * rsz;
float b = 2 * (lO.x * lD.x * rsx - lO.y * lD.y * rsy + lO.z * lD.z * rsz);
float c = lO.x*lO.x * rsx - lO.y*lO.y * rsy + lO.z*lO.z * rsz - typeParam;
return quadraticFormula(a, b, c);
}To visualise this intersection change the intersection information in our visualise shader to the following. I’ve used _ShapeParams.w for the type parameter.
// Intersect information
float2 intersect = intersectHyperboloid(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, _ShapeParams.xyz, _ShapeParams.w);
float frontIntersection = intersect.x >= 0 ? intersect.x : intersect.y;
if(frontIntersection < maxLineDst && frontIntersection >= 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * frontIntersection;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
2.4 Paraboloid
I’m not sure how useful the paraboloids are for raytracing, but they are a quadric so I’ve added them here for completeness. Paraboloids also have a type parameter where \(s_t = 1\) describes an elliptic paraboloid and \(s_t = -1\) describes a hyperbolic paraboloid. The equation for hyperboloids is given by the following [3]:
The sign function returns -1 if negative, 1 if positive and 0 if 0. By substituting the line equation we get:
Refactoring this equation results in a quadratic function of form \(a t^2 + b t + c = 0\), with the following coefficients:
Using the quadratic formula we can find up to two intersections. The code below shows how this is implemented in HLSL. As input we provide the line origin, line direction, shape origin, shape forward direction, shape up direction, the scale parameters \(s_x\) and \(s_z\), and the type parameter \(s_t\). Add the following lines to our HLSL file below the intersectHyperboloid function.
// Based on quadrics equations from https://en.wikipedia.org/wiki/Quadric
float2 intersectParaboloid(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeForwardDir, float3 shapeUpDir, float2 scaleParams, float typeParam)
{
// Transform line origin and direction from world space to the shape space
float3x3 transitionMatrix = constructTransitionMatrix(shapeForwardDir, shapeUpDir);
float3 lO = mul(transitionMatrix, lineOrigin - shapeOrigin);
float3 lD = mul(transitionMatrix, lineDir);
// Squared reciprocals of the shape parameters
float rsx = 1.0 / (scaleParams.x*scaleParams.x);
float rsz = 1.0 / (scaleParams.y*scaleParams.y);
// Sign of type parameter
float sst = sign(typeParam);
float a = lD.x*lD.x * rsx + sst * lD.z*lD.z * rsz;
float b = 2 * (lO.x * lD.x * rsx + sst * lO.z * lD.z * rsz) - lD.y ;
float c = lO.x*lO.x * rsx + sst * lO.z*lO.z * rsz - lO.y;
return quadraticFormula(a, b, c);
}To visualise this intersection change the intersection information in our visualise shader to the following.
// Intersect information
float2 intersect = intersectParaboloid(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, _ShapeParams.xz, _ShapeParams.w);
float frontIntersection = intersect.x >= 0 ? intersect.x : intersect.y;
if(frontIntersection < maxLineDst && frontIntersection >= 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * frontIntersection;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
3 Conditions and combinations
We’ve seen quite a few useful shapes, but we can make them even more versatile. One thing we can do is add additional conditions, like limiting the plane to be within a certain radius to form a circle or ellipse. Another thing would be to combine shapes, like using planes/ellipses to add caps to the cylinder, ellipsoid and hyperboloid. The following sections will shortly discuss some conditions/combinations and show how it is implemented in HLSL.
3.1 Ellipse
The ellipse is the simplest of combinations as it is a plane where we check if the intersection is within the bounds of an ellipse. The surface of an ellipse is described by following equation:
To check if a point is within the ellipse we substitute the x and z coordinate with our plane intersection coordinates.
The HLSL implementation for the ellipse thus starts the same as the plane. Only the end is different where check if the intersection point is within an ellipse, if it is we return the intersection, if not we return the max float. As input we provide the line origin, line direction, shape origin, shape forward direction, shape up direction, and the scale parameters \(s_x\) and \(s_z\) that define the ellipse. Add the following lines to our HLSL file below the intersectParaboloid function.
float intersectEllipse(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeForwardDir, float3 shapeUpDir, float2 scaleParams)
{
// Transform line origin and direction from world space to the shape space
float3x3 transitionMatrix = constructTransitionMatrix(shapeForwardDir, shapeUpDir);
float3 lO = mul(transitionMatrix, lineOrigin - shapeOrigin);
float3 lD = mul(transitionMatrix, lineDir);
float denominator = lD.y;
float numerator = lO.y;
float pIntersect = - numerator / denominator;
float3 samplePos = lO + lD * pIntersect;
bool isInEllipse = samplePos.x * samplePos.x / (scaleParams.x * scaleParams.x) + samplePos.z * samplePos.z / (scaleParams.y * scaleParams.y) <= 1;
return isInEllipse ? pIntersect : maxLineDst;
}To visualise this intersection change the intersection information in our visualise shader to the following.
// Intersect information
float intersect = intersectEllipse(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, _ShapeParams.xz);
if(intersect < maxLineDst && intersect > 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * intersect;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
3.2 Capped cylinder
Now that we have the ellipse function we can use it for other things like a capped cylinder, which consists of the infinite elliptical cylinder and two ellipses as caps.
To cap the cylinder we define it’s height through a scale parameter \(s_y\), meaning that the top cap is located at \(y = 0.5 s_y\) and the bottom cap at \(y = -0.5 s_y\). Anything above the top cap or below the bottom cap is no longer part of the shape.
In order to implement this we will first do the elliptical cylinder intersection and check if this intersection is between the caps, if not we set the distance to the max float. Next we’ll calculate the intersections for both ellipses and compare all 4 possible intersections. Luckily a capped cylinder can only have 2 intersections, the other 2 possible intersections will return the max float. Thus we can calculate and return the minimum and maximum distance intersections and return the 2 values like all our other functions.
The HLSL implementation follows the method above. As input we provide the line origin, line direction, shape origin, shape forward direction, shape up direction, and the scale parameters \(s_x\), \(s_y\) and \(s_z\), where \(s_x\) and \(s_z\) define the scales for both the cylinder and the ellipses and \(s_y\) the height of the cylinder. Add the following lines to our HLSL file below the intersectEllipse function.
float2 intersectCappedCylinder(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeForwardDir, float3 shapeUpDir, float3 scaleParams)
{
// Cylinder intersections
float2 cylinderDst = intersectEllipticCylinder(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, scaleParams.xz);
// Cylinder intersect positions
float3 samplePos1 = lineOrigin + lineDir * cylinderDst.x;
float3 samplePos2 = lineOrigin + lineDir * cylinderDst.y;
bool isMinDstBelowCap = dot(samplePos1 - shapeOrigin, shapeUpDir) <= -0.5 * scaleParams.y;
bool isMinDstAboveCap = dot(samplePos1 - shapeOrigin, shapeUpDir) >= 0.5 * scaleParams.y;
bool isMaxDstBelowCap = dot(samplePos2 - shapeOrigin, shapeUpDir) <= -0.5 * scaleParams.y;
bool isMaxDstAboveCap = dot(samplePos2 - shapeOrigin, shapeUpDir) >= 0.5 * scaleParams.y;
float minDst = cylinderDst.x;
float maxDst = cylinderDst.y;
if(isMinDstBelowCap || isMinDstAboveCap)
{
minDst = maxLineDst;
}
if(isMaxDstBelowCap || isMaxDstAboveCap)
{
maxDst = maxLineDst;
}
// Cap positions
float3 ellipse1Pos = shapeOrigin - shapeUpDir * 0.5 * scaleParams.y;
float3 ellipse2Pos = shapeOrigin + shapeUpDir * 0.5 * scaleParams.y;
// Ellipse bottom and top cap intersections
float ellipse1Dst = intersectEllipse(lineOrigin, lineDir, ellipse1Pos, shapeForwardDir, shapeUpDir, scaleParams.xz);
float ellipse2Dst = intersectEllipse(lineOrigin, lineDir, ellipse2Pos, shapeForwardDir, shapeUpDir, scaleParams.xz);
// Compare cylinder intersects to ellipse intersects for minDst
minDst = min(min(ellipse1Dst, ellipse2Dst), minDst);
// If value is maxLineDst make -maxLineDst for max comparison to work
ellipse1Dst = ellipse1Dst == maxLineDst ? -maxLineDst : ellipse1Dst;
ellipse2Dst = ellipse2Dst == maxLineDst ? -maxLineDst : ellipse2Dst;
maxDst = maxDst == maxLineDst ? -maxLineDst : maxDst;
// Compare cylinder intersects to ellipse intersects for maxDst
// and make sure we don't return -maxLineDst
maxDst = max(max(ellipse1Dst, ellipse2Dst), maxDst);
maxDst = maxDst == -maxLineDst ? maxLineDst : maxDst;
return float2(minDst, maxDst);
}To visualise this intersection change the intersection information in our visualise shader to the following.
// Intersect information
float2 intersect = intersectCappedCylinder(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, _ShapeParams.xyz);
float frontIntersection = intersect.x >= 0 ? intersect.x : intersect.y;
if(frontIntersection < maxLineDst && frontIntersection >= 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * frontIntersection;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
A slightly different version of the capped cylinder was used in my supermassive black hole shader. There it was used to describe the accretion disc circling around the centre of the black hole. The only difference being an additional condition of an inner radius, where there is no cylinder or ellipse in the middle.
3.3 Capped ellipsoid
The capped ellipsoid is slightly different, as the scale of of the caps change with their heights. A cap at the centre of the ellipsoid will be greater than that of a cap at the ends. Luckily we can calculate the height dependent ellipse scales using the equation for an ellipsoid from section 2.2. This is done by setting either x or z to 0 and solve for the other as well as putting in your cap’s height as y position. From the ellipsoid equation this results in the following [4]:
Here \(s_{e,x}\) denotes the x-scale parameter of the ellipse, \(s_x\) the x-scale parameter of the ellipsoid and \(h\) the height position of the cap. Note that, because an ellipsoid has a finite height determined by \(s_y\), we can remap it to a range of -1 to 1 range (-1 being the bottom of the ellipsoid and 1 the top) which is nicer to handle. In that case the equations would be of form \(s_{e,x} = s_x \sqrt{1 - h^2}\), with the new \(h\) between -1 and 1.
The HLSL implementation is similar to the capped cylinder, meaning we first find the ellipsoid intersections and check if they are between the caps followed by a comparison with the two ellipses. As input we provide the line origin, line direction, shape origin, shape forward direction, shape up direction, the scale parameters \(s_x\), \(s_y\) and \(s_z\), and two cap heights which get clamped between -1 and 1. Add the following lines to our HLSL file below the intersectCappedCylinder function.
float2 intersectCappedEllipsoid(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeForwardDir, float3 shapeUpDir, float3 scaleParams, float2 capHeight)
{
// Ellipsoid intersections
float2 ellipsoidDst = intersectEllipsoid(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, scaleParams);
// Cap heights in -1 to 1 range
float cap1Height = clamp(min(capHeight.x, capHeight.y), -1, 1);
float cap2Height = clamp(max(capHeight.x, capHeight.y), -1, 1);
// Ellipsoid intersect positions
float3 samplePos1 = lineOrigin + lineDir * ellipsoidDst.x;
float3 samplePos2 = lineOrigin + lineDir * ellipsoidDst.y;
bool isMinDstBelowCap = dot(samplePos1 - shapeOrigin, shapeUpDir) <= cap1Height * scaleParams.y;
bool isMinDstAboveCap = dot(samplePos1 - shapeOrigin, shapeUpDir) >= cap2Height * scaleParams.y;
bool isMaxDstBelowCap = dot(samplePos2 - shapeOrigin, shapeUpDir) <= cap1Height * scaleParams.y;
bool isMaxDstAboveCap = dot(samplePos2 - shapeOrigin, shapeUpDir) >= cap2Height * scaleParams.y;
float minDst = ellipsoidDst.x;
float maxDst = ellipsoidDst.y;
if(isMinDstBelowCap || isMinDstAboveCap)
minDst = maxLineDst;
if(isMaxDstBelowCap || isMaxDstAboveCap)
maxDst = maxLineDst;
// Cap positions
float3 ellipse1Pos = shapeOrigin + cap1Height * scaleParams.y * shapeUpDir;
float3 ellipse2Pos = shapeOrigin + cap2Height * scaleParams.y * shapeUpDir;
// Ellipsoidal cap radius from https://keisan.casio.com/keisan/image/volume%20of%20an%20ellipsoidal%20cap.pdf
float e1HeightSqr = cap1Height * cap1Height;
float e1ScaleX = scaleParams.x * sqrt(1 - e1HeightSqr);
float e1ScaleZ = scaleParams.z * sqrt(1 - e1HeightSqr);
float e2HeightSqr = cap2Height * cap2Height;
float e2ScaleX = scaleParams.x * sqrt(1 - e2HeightSqr);
float e2ScaleZ = scaleParams.z * sqrt(1 - e2HeightSqr);
// Ellipse bottom and top cap intersections
float ellipse1Dst = intersectEllipse(lineOrigin, lineDir, ellipse1Pos, shapeForwardDir, shapeUpDir, float2(e1ScaleX, e1ScaleZ));
float ellipse2Dst = intersectEllipse(lineOrigin, lineDir, ellipse2Pos, shapeForwardDir, shapeUpDir, float2(e2ScaleX, e2ScaleZ));
// Compare ellipsoid intersects to ellipse intersects for minDst
minDst = min(min(ellipse1Dst, ellipse2Dst), minDst);
// If value is maxLineDst make -maxLineDst for max comparison to work
ellipse1Dst = ellipse1Dst == maxLineDst ? -maxLineDst : ellipse1Dst;
ellipse2Dst = ellipse2Dst == maxLineDst ? -maxLineDst : ellipse2Dst;
maxDst = maxDst == maxLineDst ? -maxLineDst : maxDst;
// Compare ellipsoid intersects to ellipse intersects for maxDst
// and make sure we don't return -maxLineDst
maxDst = max(max(ellipse1Dst, ellipse2Dst), maxDst);
maxDst = maxDst == -maxLineDst ? maxLineDst : maxDst;
return float2(minDst,maxDst);
}To visualise this intersection change the intersection information in our visualise shader to the following. We use the _CapHeights float2 property to set the heights of the caps.
// Intersect information
float2 intersect = intersectCappedEllipsoid(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, _ShapeParams.xyz, _CapHeights);
float frontIntersection = intersect.x >= 0 ? intersect.x : intersect.y;
if(frontIntersection < maxLineDst && frontIntersection >= 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * frontIntersection;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
The capped ellipsoid function was used in my potions showcase, where the volume of the potion is a sphere with a single cap. The shape (and thus cap) direction was handled by a separate c# script on the gameObject that modifies shapeUpDir.
3.4 Capped half hyperboloid
Note that the name states half a hyperboloid. This is because a capped hyperboloid can have up to 4 intersections and handling that is outside the scope of this tutorial. As such we will be looking at only the lower half (\(y <= 0\)) of the hyperboloid, which has only 2 intersections.
The caps of a hyperboloid are again made of ellipses. We can calculate the height dependent ellipse scales similarly to the ellipsoid’s. This is done by taking the equation for hyperboloids from section 2.3 and setting either x or z to 0 and solve for the other. From the hyperboloid equation this results in the following:
Here \(s_{e,x}\) denotes the x-scale parameter of the ellipse, \(s_x\) the x-scale parameter of the hyperboloid, \(s_t\) the type parameter of the hyperboloid and \(h\) the height position of the cap. Because we’re only looking at the lower half of the hyperboloid we have the extra condition that \(h \leq 0\).
The HLSL implementation is again similar to the capped cylinder and capped ellipsoid, meaning we first find the hyperboloid intersections and check if they are between the caps followed by a comparison with the two ellipses. As input we provide the line origin, line direction, shape origin, shape forward direction, shape up direction, the scale parameters \(s_x\), \(s_y\) and \(s_z\), type parameter \(s_t\), and two cap heights which get clamped between -maxLineDst and 0. Add the following lines to our HLSL file below the intersectCappedEllipsoid function.
float2 intersectCappedHalfHyperboloid(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeForwardDir, float3 shapeUpDir, float3 scaleParams, float typeParam, float2 capHeight)
{
// Hyperboloid intersections
float2 hyperboloidDst = intersectHyperboloid(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, scaleParams, typeParam);
// Cap heights in -maxLineDst to 0 range
float cap1Height = clamp(min(capHeight.x, capHeight.y), -maxLineDst, 0);
float cap2Height = clamp(max(capHeight.x, capHeight.y), -maxLineDst, 0);
// Ellipsoid intersect positions
float3 samplePos1 = lineOrigin + lineDir * hyperboloidDst.x;
float3 samplePos2 = lineOrigin + lineDir * hyperboloidDst.y;
bool isMinDstBelowCap = dot(samplePos1 - shapeOrigin, shapeUpDir) <= cap1Height;
bool isMinDstAboveCap = dot(samplePos1 - shapeOrigin, shapeUpDir) >= cap2Height;
bool isMaxDstBelowCap = dot(samplePos2 - shapeOrigin, shapeUpDir) <= cap1Height;
bool isMaxDstAboveCap = dot(samplePos2 - shapeOrigin, shapeUpDir) >= cap2Height;
float minDst = hyperboloidDst.x;
float maxDst = hyperboloidDst.y;
if(isMinDstBelowCap || isMinDstAboveCap)
minDst = maxLineDst;
if(isMaxDstBelowCap || isMaxDstAboveCap)
maxDst = maxLineDst;
// Cap positions
float3 ellipse1Pos = shapeOrigin + cap1Height * shapeUpDir;
float3 ellipse2Pos = shapeOrigin + cap2Height * shapeUpDir;
// Hyperboloid cap radius
float sySqrR = 1 / (scaleParams.y * scaleParams.y);
float e1HeightSqr = cap1Height * cap1Height;
float e1ScaleX = scaleParams.x * sqrt(typeParam + e1HeightSqr * sySqrR);
float e1ScaleZ = scaleParams.z * sqrt(typeParam + e1HeightSqr * sySqrR);
float e2HeightSqr = cap2Height * cap2Height;
float e2ScaleX = scaleParams.x * sqrt(typeParam + e2HeightSqr * sySqrR);
float e2ScaleZ = scaleParams.z * sqrt(typeParam + e2HeightSqr * sySqrR);
// Ellipse bottom and top cap intersections
float ellipse1Dst = intersectEllipse(lineOrigin, lineDir, ellipse1Pos, shapeForwardDir, shapeUpDir, float2(e1ScaleX, e1ScaleZ));
float ellipse2Dst = intersectEllipse(lineOrigin, lineDir, ellipse2Pos, shapeForwardDir, shapeUpDir, float2(e2ScaleX, e2ScaleZ));
// Compare ellipsoid intersects to ellipse intersects for minDst
minDst = min(min(ellipse1Dst, ellipse2Dst), minDst);
// If value is maxLineDst make -maxLineDst for max comparison to work
ellipse1Dst = ellipse1Dst == maxLineDst ? -maxLineDst : ellipse1Dst;
ellipse2Dst = ellipse2Dst == maxLineDst ? -maxLineDst : ellipse2Dst;
maxDst = maxDst == maxLineDst ? -maxLineDst : maxDst;
// Compare ellipsoid intersects to ellipse intersects for maxDst
// and make sure we don't return -maxLineDst
maxDst = max(max(ellipse1Dst, ellipse2Dst), maxDst);
maxDst = maxDst == -maxLineDst ? maxLineDst : maxDst;
return float2(minDst,maxDst);
}To visualise this intersection change the intersection information in our visualise shader to the following.
// Intersect information
float2 intersect = intersectCappedHalfHyperboloid(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, _ShapeParams.xyz, _ShapeParams.w, _CapHeights);
float frontIntersection = intersect.x >= 0 ? intersect.x : intersect.y;
if(frontIntersection < maxLineDst && frontIntersection >= 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * frontIntersection;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
3.5 Rectangle
The rectangle is very similar to the ellipse, in that we do a plane intersection and check if it is within the bounds of a rectangle. The rectangular surface is bounded by the following 2 conditions:
Here \(|x|\) stands for the absolute value of x. To check if a point is within the rectangle we substitute the x and z coordinate with our plane intersection coordinates.
The HLSL implementation for the rectangle thus starts the same as the plane. Only the end is different where check if the intersection point is within an rectangle, if it is we return the intersection, if not we return the max float. As input we provide the line origin, line direction, shape origin, shape forward direction, shape up direction, and the scale parameters \(s_x\) and \(s_z\) that define the bounds of the rectangle. Note that the rectangle’s length is \(2 s_x\). Add the following lines to our HLSL file below the intersectCappedHalfHyperboloid function.
float intersectRectangle(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeForwardDir, float3 shapeUpDir, float2 scaleParams)
{
// Transform line origin and direction from world space to the shape space
float3x3 transitionMatrix = constructTransitionMatrix(shapeForwardDir, shapeUpDir);
float3 lO = mul(transitionMatrix, lineOrigin - shapeOrigin);
float3 lD = mul(transitionMatrix, lineDir);
float denominator = lD.y;
float numerator = lO.y;
float pIntersect = - numerator / denominator;
float3 samplePos = lO + lD * pIntersect;
bool isInRectangle = abs(samplePos.x) <= scaleParams.x && abs(samplePos.z) <= scaleParams.y;
return isInRectangle ? pIntersect : maxLineDst;
}To visualise this intersection change the intersection information in our visualise shader to the following.
// Intersect information
float intersect = intersectRectangle(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, _ShapeParams.xz);
if(intersect < maxLineDst && intersect > 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * intersect;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
3.6 Box
A box simply consists of 6 rectangles that each form a face. In this section we will find the intersection of a box through comparing 6 rectangle intersections, but I want to let you know that this is not the most optimal way of finding box intersections. If you are looking for a more optimal way I’d suggest looking at the boxIntersection function by Inigo Quilez.
For our approach there isn’t really more to it than doing a rectangle intersection for the up, down, forward, backward, right and left face of the box. You only need to remind yourself what the rectangle’s up direction and origin would be, and how the scale parameters should be ordered with respect to the forward direction.
The HLSL implementation thus consists of 6 rectangle intersections, which are then compared using min and max functions. As input we provide the line origin, line direction, shape origin, shape forward direction, shape up direction, and the scale parameters \(s_x\), \(s_y\) and \(s_z\) that define the bounds of the box. Note that the box’s length is \(2 s_x\). Add the following lines to our HLSL file below the intersectCappedHalfHyperboloid function.
float2 intersectBox(float3 lineOrigin, float3 lineDir, float3 shapeOrigin, float3 shapeForwardDir, float3 shapeUpDir, float3 scaleParams)
{
// Calculate right direction
float3 shapeRightDir = cross(shapeForwardDir, shapeUpDir);
// Rectangle face intersections
float faceUp = intersectRectangle(lineOrigin, lineDir, shapeOrigin + shapeUpDir * scaleParams.y, shapeForwardDir, shapeUpDir, scaleParams.xz);
float faceDown = intersectRectangle(lineOrigin, lineDir, shapeOrigin - shapeUpDir * scaleParams.y, shapeForwardDir, shapeUpDir, scaleParams.xz);
float faceForward = intersectRectangle(lineOrigin, lineDir, shapeOrigin + shapeForwardDir * scaleParams.z, -shapeUpDir, shapeForwardDir, scaleParams.xy);
float faceBackward = intersectRectangle(lineOrigin, lineDir, shapeOrigin - shapeForwardDir * scaleParams.z, -shapeUpDir, shapeForwardDir, scaleParams.xy);
float faceRight = intersectRectangle(lineOrigin, lineDir, shapeOrigin + shapeRightDir * scaleParams.x, shapeForwardDir, shapeRightDir, scaleParams.yz);
float faceLeft = intersectRectangle(lineOrigin, lineDir, shapeOrigin - shapeRightDir * scaleParams.x, shapeForwardDir, shapeRightDir, scaleParams.yz);
// Min face comparison
float minDst = min(faceUp,min(faceDown,min(faceForward,min(faceBackward, min(faceRight, faceLeft)))));
// If value is maxLineDst make -maxLineDst for max comparison to work
faceUp *= faceUp == maxLineDst ? -1 : 1;
faceDown *= faceDown == maxLineDst ? -1 : 1;
faceForward *= faceForward == maxLineDst ? -1 : 1;
faceBackward *= faceBackward == maxLineDst ? -1 : 1;
faceRight *= faceRight == maxLineDst ? -1 : 1;
faceLeft *= faceLeft == maxLineDst ? -1 : 1;
// Maxn face comparison and make sure we don't return -maxLineDst
float maxDst = max(faceUp,max(faceDown,max(faceForward,max(faceBackward, max(faceRight, faceLeft)))));
maxDst *= maxDst == -maxLineDst ? -1 : 1;
return float2(minDst, maxDst);
}To visualise this intersection change the intersection information in our visualise shader to the following.
// Intersect information
float2 intersect = intersectBox(lineOrigin, lineDir, shapeOrigin, shapeForwardDir, shapeUpDir, _ShapeParams.xyz);
float frontIntersection = intersect.x >= 0 ? intersect.x : intersect.y;
if(frontIntersection < maxLineDst && frontIntersection >= 0)
{
float3 pos = lineOrigin - shapeOrigin + lineDir * frontIntersection;
r = saturate(abs(pos.x)/_DistanceScale);
g = saturate(abs(pos.y)/_DistanceScale);
b = saturate(abs(pos.z)/_DistanceScale);
}
4 Conclusion
While there are still more combinations to add to this list I think 11 shape functions is a good start. This tutorial in of itself is obviously not that exiting from a visual perspective, but these functions can be used to create more interesting shaders like my black hole shader or potion shader. Be sure to show me your shaders that implement these functions by tagging me on twitter (@kelvinvanhoorn) or on reddit (u/Radagasd). Also, while not necessary I’ll very much appreciate it if you credit me when using these functions in your projects.
I do want to emphasise that while these functions give the correct answer, they aren’t necessarily the most optimal way (computation-wise) of getting there. If you’re interested you could take a look at Inigo Quilez’s functions here that covers most functions in a more optimal way.
Thank you very much for reading and I hope you learned something new. If you want to support me financially you can do so using my ko-fi page.
References
- Plane equation from Wikipedia’s page on planes.
- Images made by Sam Derbyshire found on Wikipedia’s page on quadric surfaces.
- Equations for real quadric surfaces in Euclidean space from Wikipedia’s page on quadrics.
- Overview of finding the ellipses on an ellipsoid by Keisan